힙 Heap

[2022.09.18] 모각코에서 힙이 기억나냐고 물었는데 '이진 트리..'라고 밖에 설명 못해서 자극 받음.

힙 Heap

• 완전 이진 트리의 일종으로 우선순위 큐를 위하여 만들어진 자료구조.
• 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.
• 최댓값이나 최솟값을 빠르게 찾아내도록 만들어짐.
• 일종의 반정렬 상태(느슨한 정렬 상태)
• 큰 값이 상위 레벨에 있고 작은 값이 하위 레벨에 있다는 정도
• 힙 트리에서는 중복된 값을 허용한다. (이진 탐색 트리에서는 중복된 값을 허용하지 않는다.)

시간복잡도

• 탐색 및 연산 시간복잡도 : $O(logn)$
  이진트리의 말단 노드에 값이 있다면 높이($h$)만큼 탐색해야 함.
  [안드로이드](안드로이드 Android)

$$
시간복잡도 = O(h)
$$
완전이진트리이므로
$$
\begin{align}
(2^{(h-1)}-1) +1 \leq ;&n \leq 2^h-1\\log(n+1) \leq ;&h \leq logn + 1 \\\end{align}
$$
따라서,
$$
시간복잡도 = O(h) = O(logn+1) = O(logn)
$$

• 힙 정렬 시간복잡도 : $O(nlogn)$
  n개의 노드가 각각 heapify해야 함.

힙의 종류

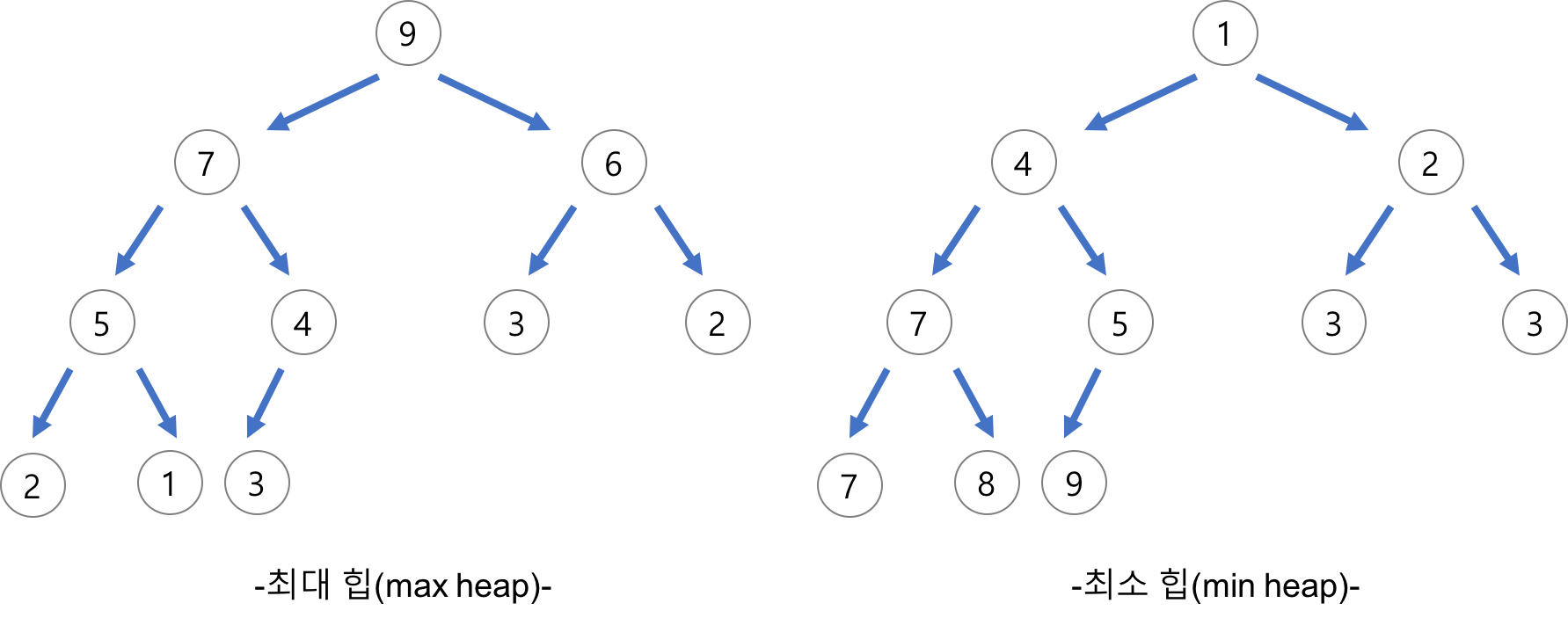
활용 알고리즘 문제 유형

1. N번째 큰 수/작은 수
2. 중간값 구하기 (Two heaps)
3. k개의 배열 합치기
4. 최소값

References

• 위키백과 - 힙 (자료 구조) https://ko.wikipedia.org/wiki/힙_(자료_구조)
• [자료구조] 힙(heap)이란 https://gmlwjd9405.github.io/2018/05/10/data-structure-heap.html
• 모각코 '재개발코딩' annyeong님 발표자료 : <안키워요 - JS heap>